某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件．投入市场后，游戏软件的利润占这4款软件总利润的 ．如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图．
根据以上信息，回答下列问题
（1）直接写出图中 ， 的值；
（2）分别求网购与视频软件的人均利润；
（3）在总人数和各款软件人均利润都保持不变的情况下，能否只调整网购与视频软件的研发与维护人数，使总利润增加60万元？如果能，写出调整方案；如果不能，请说明理由．
如图，点C是l上任意一点，CA⊥CB且AC＝BC，过点A作AM⊥l于点M，过点B作BN⊥l于N，则线段MN与AM、BN有什么数量关系，证明你的结论：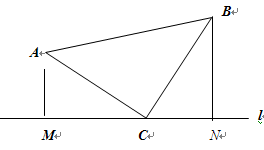
已知：A＝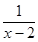
，B＝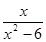
，当x为何值时，A与B的值相等？
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度y (cm)是椅子的高度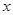
（cm）的一次函数,下表列出两套符合条件的课桌椅的高度: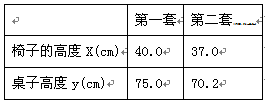 
（1）请确定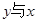
的函数关系式;
（2）现有一把高39cm的椅子，按上述函数关系，与它相配套的桌子的高度应为多少cm？
小明家的阳台地面，水平铺设着仅颜色不同的18块黑色方砖（如图11所示），他从房间里向阳台抛小皮球，小皮球最终随机停留在某块方砖上. 
（1）求小皮球分别停在黑色方砖和白色方砖上的概率；
（2）上述哪个概率较大？要使这两个概率相等，应改变第几行第几列的哪块方砖颜色？怎样改变？
如图，直线DE交△ABC的边AB、AC于D、E，交BC的延长线于点F，若∠B＝67°，∠ACB＝74°，∠AED＝48°，求∠BDF的度数。