如图,1号楼在2号楼的南侧,两楼高度均为 ,楼间距为 .冬至日正午,太阳光线与水平面所成的角为 ,1号楼在2号楼墙面上的影高为 ;春分日正午,太阳光线与水平面所成的角为 ,1号楼在2号楼墙面上的影高为 .已知 .
(1)求楼间距 ;
(2)若2号楼共30层,层高均为 ,则点 位于第几层?(参考数据: , , , , ,

如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79,sin22°≈0.37,cos22°≈0.93,sin37°≈0.60,cos37°≈0.80)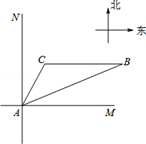
某工程队承接了3000米的修路任务,在修好600米后,引进了先进设备,工作效率是原来的2倍,一共用了30天完成任务,求引进新设备前每天平均修路多少米.
在一个不透明的盒子里,装有三个分别写有数字6, 2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
(满分14分)如图,抛物线经过 (
( ),
), (
( ),
), (
( )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点 ,使
,使 的值最小,求点
的值最小,求点 的坐标;
的坐标;
(3)点 为
为 轴上一动点,在抛物线上是否存在点
轴上一动点,在抛物线上是否存在点 ,使得以
,使得以 四点为顶点的四边形为平行四边形?若存在,请直接写出点
四点为顶点的四边形为平行四边形?若存在,请直接写出点 的坐标.
的坐标.
(满分14分)如图,已知 ,
, ,点
,点 从点
从点 开始沿
开始沿 边向点
边向点 以
以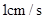 的速度移动,点
的速度移动,点 从点
从点 开始向点
开始向点 以相同的速度移动,若
以相同的速度移动,若 、
、 同时出发,移动时间为
同时出发,移动时间为 (0≤
(0≤ ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线 翻折后得到
翻折后得到 ,试判断点
,试判断点 是否落在直线
是否落在直线 上,并说明理由.
上,并说明理由.
(3)当 为何值时,
为何值时, 与
与 相似.
相似.