解方程（组）：
（1）4－3x＝6－5x；（2）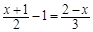
；（3）
．
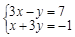先化简，再求值：2m2－4m＋1－2（m2＋2m－
），其中m＝－1．
用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有38张硬纸板，裁剪时x张用A方法，其余用B方法。
（1）用x的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
已知：AB∥CD，∠B +∠D＝
，判断直线BC与ED的位置关系并请说明理由．
如图，O为直线AB上一点，OD平分∠AOC，∠DOE＝
．
（1）若∠AOC＝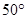
，求出∠BOD的的度数；
（2）试判断OE是否平分∠BOC，并说明理由．