如图1,平行四边形 中, , , ,点 在边 上运动,以 为圆心, 为半径的 与对角线 交于 , 两点.
(1)如图2,当 与边 相切于点 时,求 的长;
(2)不难发现,当 与边 相切时, 与平行四边形 的边有三个公共点,随着 的变化, 与平行四边形 的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的 的值的取值范围 .
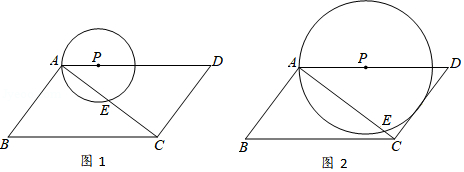
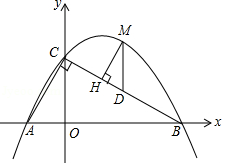
如图,直线 分别与 轴、 轴交于 、 两点,点 在 轴上, ,抛物线 经过 , 两点.
(1)求 、 两点的坐标;
(2)求抛物线的解析式;
(3)点 是直线 上方抛物线上的一点,过点 作 于点 ,作 轴交 于点 ,求 周长的最大值.
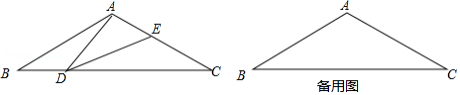
如图,在等腰三角形 中, , ,点 是 边上的一个动点(不与 、 重合),在 上取一点 ,使 .
(1)求证: ;
(2)设 , ,求 关于 的函数关系式并写出自变量 的取值范围;
(3)当 是等腰三角形时,求 的长.
为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对 、 两类学校进行改扩建,根据预算,改扩建2所 类学校和3所 类学校共需资金7800万元,改扩建3所 类学校和1所 类学校共需资金5400万元.
(1)改扩建1所 类学校和1所 类学校所需资金分别是多少万元?
(2)该县计划改扩建 、 两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到 、 两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
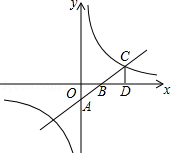
如图,一次函数 的图象与坐标轴分别交于 、 两点,与反比例函数 的图象在第一象限的交点为 , 轴,垂足为 ,若 , , 的面积为3.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当 时, 的解集.
如图,在 中, ,以 为直径的 交 于点 ,过点 作 的切线 ,交 于点 , 的反向延长线交 于点 .
(1)求证: ;
(2)若 , 的半径为10,求 的长度.
