在 中, , 交 的延长线于点 .

特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为 ,一条直角边与 重合,另一条直角边恰好经过点 .通过观察、测量 与 的长度,得到 .请给予证明.
猜想论证:
(2)当三角尺沿 方向移动到图2所示的位置时,一条直角边仍与 边重合,另一条直角边交 于点 ,过点 作 垂足为 .此时请你通过观察、测量 、 与 的长度,猜想并写出 、 与 之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿 方向继续移动到图3所示的位置(点 在线段 上,且点 与点 不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
已知抛物线 与 轴相交于 , 两点,与 轴交于点 ,点 是 轴上的动点.
(1)求抛物线的解析式;
(2)如图1,若 ,过点 作 轴的垂线交抛物线于点 ,交直线 于点 .过点 作 于点 ,当 为何值时, ;
(3)如图2,将直线 绕点 顺时针旋转,它恰好经过线段 的中点,然后将它向上平移 个单位长度,得到直线 .
① ;
②当点 关于直线 的对称点 落在抛物线上时,求点 的坐标.

红星公司销售一种成本为40元 件产品,若月销售单价不高于50元 件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为 (单位:元 件),月销售量为 (单位:万件).
(1)直接写出 与 之间的函数关系式,并写出自变量 的取值范围;
(2)当月销售单价是多少元时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款 元.已知该公司捐款当月的月销售单价不高于70元 件,月销售最大利润是78万元,求 的值.
2021年是中国共产党建党100周年,红旗中学以此为契机,组织本校师生参加红色研学实践活动,现租用甲、乙两种型号的大客车(每种型号至少一辆)送549名学生和11名教师参加此次实践活动,每辆汽车上至少要有一名教师.
甲、乙两种型号的大客车的载客量和租金如表所示:
|
甲种客车 |
乙种客车 |
|
|
载客量 (人 辆) |
40 |
55 |
|
租金 (元 辆) |
500 |
600 |
(1)共需租 辆大客车;
(2)最多可以租用多少辆甲种型号大客车?
(3)有几种租车方案?哪种租车方案最节省钱?
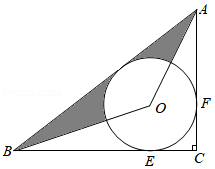
如图,在 中, , 与 , 分别相切于点 , , 平分 ,连接 .
(1)求证: 是 的切线;
(2)若 , 的半径是1,求图中阴影部分的面积.
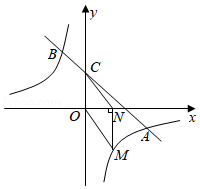
如图,反比例函数 的图象与一次函数 的图象相交于 , 两点.
(1)求反比例函数和一次函数的解析式;
(2)设直线 交 轴于点 ,点 是 轴正半轴上的一个动点,过点 作 轴交反比例函数 的图象于点 ,连接 , .若 ,求 的取值范围.