小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


如图,在⊙O中, =
=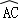 ,∠A=30°,求∠B的度数.
,∠A=30°,求∠B的度数.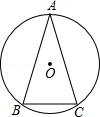
已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).求二次函数的解析式.
如图所示,已知抛物线y=x2﹣1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
已知二次函数y=﹣ x2+
x2+ x的图象如图.
x的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式.
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.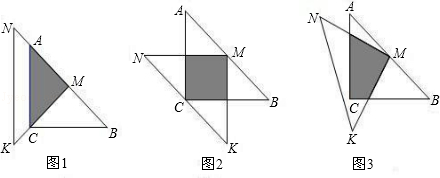
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 ;
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 ;
(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.