新冠疫情防控期间,全国中小学开展“停课不停学”活动.某市为了解初中生每日线上学习时长 (单位:小时)的情况,在全市范围内随机抽取了 名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.

根据图中信息,解答下列问题:
(1)在这次调查活动中,采取的调查方式是 (填写“全面调查”或“抽样调查” , ;
(2)从该样本中随机抽取一名初中生每日线上学习时长,其恰好在“ ”范围的概率是 ;
(3)若该市有15000名初中生,请你估计该市每日线上学习时长在“ ”范围的初中生有 名.
请把下面不完整的数轴画完整,并在数轴上标出下列各数:-3,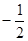 ,4.
,4.
合并同类项: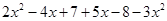 .
.
解方程: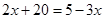 .
.
已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC=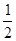 AB,则点C表示的数是;
AB,则点C表示的数是;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC= BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
电子商务的快速发展逐步改变了人们的购物方式,网购已悄然进入千家万户.李阿姨在某网店
买了甲、乙两件商品,已知甲商品的价格比乙商品价格的2倍多108元,乙商品的价格比甲、乙两件商品
总价的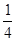 少3元.问甲、乙两件商品的价格各多少元?
少3元.问甲、乙两件商品的价格各多少元?