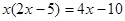如图，C为线段AB外一点．（1）求作四边形ABCD，使得CD-优题课

游客

题文

如图， $C$ 为线段 $AB$ 外一点．

（1）求作四边形 $ABCD$ ，使得 $CD / / AB$ ，且 $CD = 2 AB$ ；（要求：尺规作图，不写作法，保留作图痕迹）

（2）在（1）的四边形 $ABCD$ 中， $AC$ ， $BD$ 相交于点 $P$ ， $AB$ ， $CD$ 的中点分别为 $M$ ， $N$ ，求证： $M$ ， $P$ ， $N$ 三点在同一条直线上．

科目数学题型解答题难度中等

知识点：作图—复杂作图相似三角形的判定与性质

登录免费查看答案和解析

相关试题

△ABC为等边三角形，点D是边AB的延长线上一点（如图1），以点D为中心，将△ABC按顺时针方向旋转一定角度得到△ABC.

（1）若旋转后的图形如图2所示，请将△ABC以点O为中心，按顺时针方向再次旋转同样的角度得到△ABC，在图2中用尺规作出△ABC，请保留作图痕迹，不要求写作法：
（2）若将△ABC按顺时针方向旋转到△ABC的旋转角度为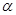(0°<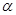<360°)．且AC∥BC，直接写出旋转角度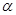的值为________________

已知关于x的一元二次方程．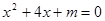
（1）当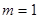时，请用配方法求方程的根：
（2）若方程没有实数根，求m的取值范围．

如图，两个圆都以点D为圆心．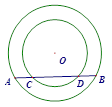

求证：AC=BD.

有两个可以自由转动的质地均匀转盘都被分成了3．个全等的扇形，在每一扇形内均标有不同的自然数，如图所示，转动转盘，两个转盘停止后观察并记录两个指针所指扇形内的数字（若指针停在扇形的边线上，当作指向上边的扇形）．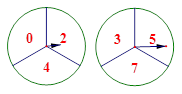

(l)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果；
(2)同时转动两个转盘一次，求“记录的两个数字之和为7”的概率．

解方程：

试卷网试题网古诗词网作文网范文网