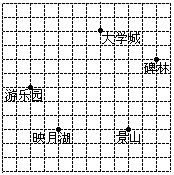
某企业承接了27000件产品的生产任务，计划安排甲、乙两个车间的共50名工人，合作生产20天完成．已知甲、乙两个车间利用现有设备，工人的工作效率为：甲车间每人每天生产25件，乙车间每人每天生产30件．
（1）求甲、乙两个车间各有多少名工人参与生产？
（2）为了提前完成生产任务，该企业设计了两种方案：
方案一 甲车间租用先进生产设备，工人的工作效率可提高 ，乙车间维持不变．
方案二 乙车间再临时招聘若干名工人（工作效率与原工人相同），甲车间维持不变．
设计的这两种方案，企业完成生产任务的时间相同．
①求乙车间需临时招聘的工人数；
②若甲车间租用设备的租金每天900元，租用期间另需一次性支付运输等费用1500元；乙车间需支付临时招聘的工人每人每天200元．问：从新增加的费用考虑，应选择哪种方案能更节省开支？请说明理由．
在平面直角坐标系xOy中，已知A（2，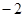
），在y轴上确定点P，使△AOP为等腰三角形，探究符合条件的点P的个数.
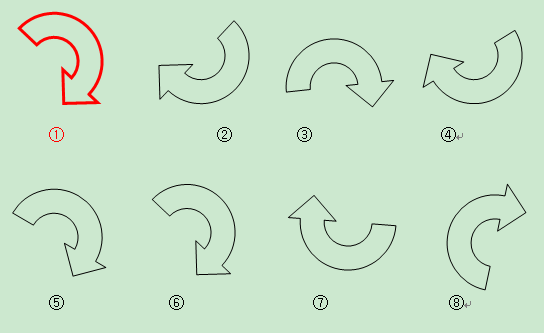
在下面的八幅图案中，②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到？
如图，已知射线DM与直线BC交于点A，AB∥DE.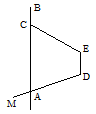
（1）若当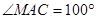
，
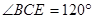时，问把EC绕点E再旋转多大角度时，可判定MD∥EC，请你设计出两种方案，并画出草图（旋转后若EC与AB相交，则交点用
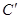表示）.
（2）若将EC绕点E逆时针旋转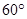
时，点C与点A恰好重合，请画出草图，并在图中找出同位角、内错角各两对（先用数字标出角，再回答）.
如图，四边形ABCD中，∠A ="∠C=" 90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由。
请你在下图中建立适当的直角坐标系，并写出各地点的坐标。。