某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题:
抽取的学生最喜爱体育锻炼项目的统计表
类别 |
项目 |
人数(人 |
|
跳绳 |
59 |
|
健身操 |
▲ |
|
俯卧撑 |
31 |
|
开合跳 |
▲ |
|
其它 |
22 |
(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.

(满分l4分)已知:抛物线y=x2-(a+2)x+9的顶点在坐标轴上.
(1)求a的值;
(2)若该抛物线的顶点C在x轴的正半轴上,而此抛物线与直线Y=x+9交于A,B两点,且A点在B点左侧,P为线段AB上的点(A,B两端点除外).过点P作x轴的垂线与抛物线交于点Q(可在图中画示意图).问:
①线段AB上是否存在这样的点P,使得PQ的长等于6?若存在,请求出点P的坐标;若不存在,请说明理由.
②线段AB上是否存在这样的点P,使得△ABQ∽△OAC?若存在,请求出此时点Q的坐标;若不存在,请说明理由.
(满分l2分)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.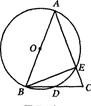
(1)求∠EBC的度数;
(2)求证:BD=CD.
(满分l2分)某中学对全校学生60s跳绳的次数进行了统计,全校学生的平均次数是l00次.某班体育委员统计了全班50名学生60s跳绳的成绩,列出的频数分布直方图如图所示(每个分组包括左端点,不包括右端点).
(1)该班60s跳绳的平均次数是多少?是否超过全校的平均次数?
(2)该班一个学生说:“我的跳绳成绩在我班是中位数.”请你给出该生跳绳成绩所在的范围.
(3)从该班中任选一人,其跳绳次数达到或超过校平均次数的概率是多少?
(满分l2分)暑假期间,小明和父母一起开车到距家200 km的景点旅游.出发前,汽车油箱内储油45L;当行驶l50 km时,发现油箱剩余油量为30 L.
(1)已知油箱内余油量y(L)是行驶路程x(km)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3 L时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
(满分l0分)如图,△ABC是等边三角形,点D是AC的中点,延长BC到点E,使CE=CD.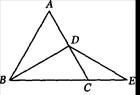
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,保留作图痕迹);
(2)求证:BM=EM.