如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

计算: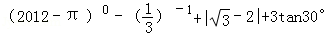 .
.
将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕。
(1)第3次对折后共有多少条折痕?第4次对折后呢?
(2)请找出折痕条数与对折次数的对应规律,写出对折n次后,折痕有多少条?
宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?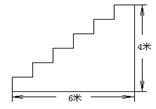
你能将-1、-2、-3、-4、0、1、2、3、4这9个数字填入图中并使每行、列,对角线上的三个数字加都相等。
如图,B、C、E三点在一条直线上,⊿ABC和⊿DCE都为等边三角形,连接AE、DB、
(1)试说出 AE=BD的理由、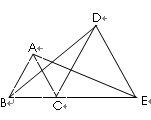
(2)如果把⊿DCE绕C点顺时针旋转一个角度,使B、C、E不在一条直线上,(1)中的结论还成立吗?(只回答,不说理由)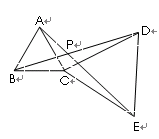
(3)在(2)中若AE、BD相交于P, 求∠APB的度数、