某水果商店销售一种进价为40元 千克的优质水果,若售价为50元 千克,则一个月可售出500千克;若售价在50元 千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元 千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
解方程: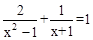
已知: ,求
,求 的值.
的值.
已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.


(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x, ,求y与x的函数关系式并写出自变量x 的取值范围。
,求y与x的函数关系式并写出自变量x 的取值范围。
(3)连接CO,若△PCO与△PCA相似,求此时BD的长。
如图,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外侧作Rt△ABE和Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,
(1)若Rt△ABE和Rt△ACF都是等腰三角形,直接写出EP与FQ有怎样的数量关系;
(2)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC=" k" AF时,(1)中的结论还成立吗?若成立,请证明;若不成立,请探究EP与FQ有怎样的数量关系?
(3)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC= mAF时,联结EF交射线GA于点D,试探究ED与FD有怎样的数量关系?
如图,已知直线l经过点A(1,0),与双曲线y=(x>0)交于点B(2,1).过点P(a,a-1)
(a>1)作x轴的平行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA.