如图，抛物线yax23ax4a的图象经过点C(0,2)，交x-优题课

如图，抛物线 $y = a x^{2} - 3 ax - 4 a$ 的图象经过点 $C (0, 2)$ ，交 $x$ 轴于点 $A$ 、 $B$ （点 $A$ 在点 $B$ 左侧），连接 $BC$ ，直线 $y = kx + 1 (k > 0)$ 与 $y$ 轴交于点 $D$ ，与 $BC$ 上方的抛物线交于点 $E$ ，与 $BC$ 交于点 $F$ ．

（1）求抛物线的解析式及点 $A$ 、 $B$ 的坐标；

（2） $\frac{EF}{DF}$ 是否存在最大值？若存在，请求出其最大值及此时点 $E$ 的坐标；若不存在，请说明理由．

科目数学题型解答题难度中等

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

在平面直角坐标系中，已知抛物线 $y ＝ x^{2} + bx + c$ 的顶点M的坐标为（﹣1，﹣4），且与x轴交于点A，点B（点A在点B的左边），与y轴交于点C．

（1）填空：b＝　　，c＝　　，直线AC的解析式为　　；

（2）直线 $x ＝ t$ 与x轴相交于点H．

①当 $t ＝﹣ 3$ 时得到直线AN（如图1），点D为直线AC下方抛物线上一点，若 $∠ COD ＝ ∠ MAN$ ，求出此时点D的坐标；

②当 $﹣ 3 ＜ t ＜﹣ 1$ 时（如图2），直线 $x ＝ t$ 与线段AC，AM和抛物线分别相交于点E，F，P．试证明线段HE，EF，FP总能组成等腰三角形；如果此等腰三角形底角的余弦值为 $\frac{3}{5}$ ，求此时t的值．

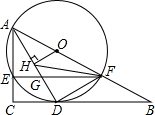
如图，在Rt△ABC中， $∠ C ＝ 90 °$ ，点O在AB上，经过点A的⊙O与BC相切于点D，与AC，AB分别相交于点E，F，连接AD与EF相交于点G．

（1）求证：AD平分∠CAB；

（2）若 $OH ⊥ AD$ 于点H，FH平分 $∠ AFE ， DG ＝ 1$ ．

①试判断DF与DH的数量关系，并说明理由；

②求⊙O的半径．

孝感市在创建国家级园林城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

（1）求A种，B种树木每棵各多少元？

（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

已知关于x的一元二次方程 $x^{2} ﹣ 2 x + m ﹣ 1 ＝ 0$ 有两个实数根x₁，x₂．

（1）求m的取值范围；

（2）当时，求m的值．

如图，在Rt△ABC中， $∠ ACB ＝ 90 °$ ．

（1）请用直尺和圆规按下列步骤作图，保留作图痕迹：

①作∠ACB的平分线，交斜边AB于点D；

②过点D作AC的垂线，垂足为点E．

（2）在（1）作出的图形中，若 $CB ＝ 4$ ， $CA ＝ 6$ ，则DE＝　　．