在平面直角坐标系中,已知抛物线 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线 与x轴相交于点H.
①当 时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若 ,求出此时点D的坐标;
②当 时(如图2),直线 与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为 ,求此时t的值.

如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.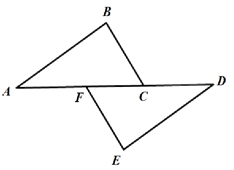
请分别画出下图中各图的所有对称轴.
(1)正方形(2)正三角形(3)相交的两个圆
如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一条直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF;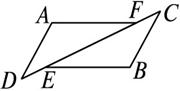
(1)请你用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题;(用序号写出命题的书写形式,如:如果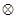
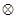 ,那么
,那么 )
)
(2)选择(1)中你写的一个命题,说明它的正确性
如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。
(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
数学课上老师出了一道题:计算2962的值,喜欢数学的小亮举手做出这道题,他的解题过程如下:2962=(300-4)2=3002-2×300×(-4)+42=90000+2400+16=92416
老师表扬小亮积极发言的同时,也指出了解题中的错误,你认为小亮的解题过程错在哪儿,并给出正确的答案。