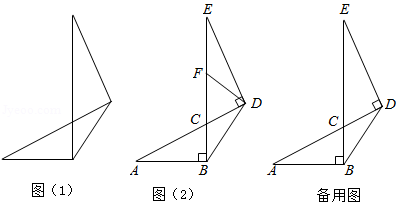
小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形, 与 恰好为对顶角, ,连接 , ,点 是线段 上一点.
探究发现:
(1)当点 为线段 的中点时,连接 (如图(2) ,小明经过探究,得到结论: .你认为此结论是否成立? .(填"是"或"否"
拓展延伸:
(2)将(1)中的条件与结论互换,即: ,则点 为线段 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若 , ,求 的长.
已知:如图,一次函数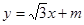 与反比例函数
与反比例函数 的图象在第一象限的交点为
的图象在第一象限的交点为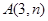 .
.
(1)求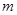 与
与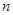 的值;
的值;
(2)设一次函数的图像与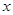 轴交于点
轴交于点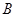 ,连接
,连接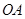 ,求
,求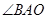 的度数.
的度数.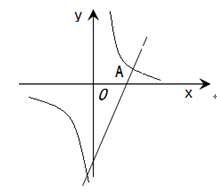
甲、乙两人准备整理一批新到的实验器材.若甲单独整理需要40分钟完工:若甲、乙共同整理20分钟后,乙需再单独整理20分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过30分钟,则甲至少整理多少分钟才能完工?
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.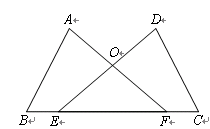
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计.结果如图1所示.
(1)在这次调查中,一共抽查了名学生;
(2)求出扇形统计图(图2)中参加“音乐活动”项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术活动项目的人数.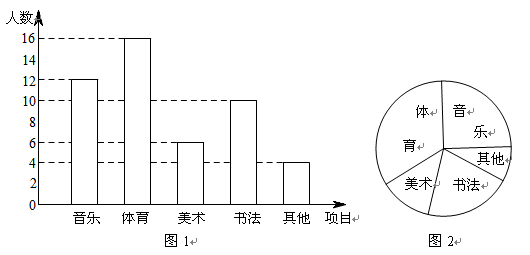
已知关于x的一元二次方程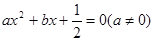 有两个相等的实数根,求
有两个相等的实数根,求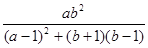 的值。
的值。