为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计.结果如图1所示.
(1)在这次调查中,一共抽查了 名学生;
(2)求出扇形统计图(图2)中参加“音乐活动”项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术活动项目的人数.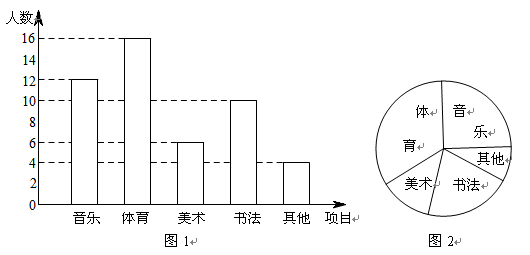
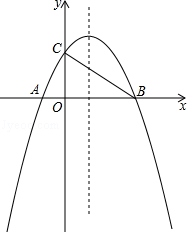
如图,在平面直角坐标系中,已知抛物线 y= ax 2+ bx+2( a≠0)与 x轴交于 A(﹣1,0), B(3,0)两点,与 y轴交于点 C,连接 BC.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点 D为抛物线对称轴上一点,连接 CD、 BD,若∠ DCB=∠ CBD,求点 D的坐标;
(3)已知 F(1,1),若 E( x, y)是抛物线上一个动点(其中1< x<2),连接 CE、 CF、 EF,求△ CEF面积的最大值及此时点 E的坐标.
(4)若点 N为抛物线对称轴上一点,抛物线上是否存在点 M,使得以 B, C, M, N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点 M的坐标;若不存在,请说明理由.
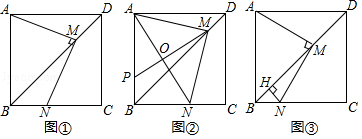
如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.
如图,在⊙ O中, B是⊙ O上的一点,∠ ABC=120°,弦 AC=2 ,弦 BM平分∠ ABC交 AC于点 D,连接 MA, MC.
(1)求⊙ O半径的长;
(2)求证: AB+ BC= BM.

某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨 .据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为1500元;旺季所有的货车每天能全部租出,日租金总收入为4000元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
如图,在四边形 ABCD中, AD∥ BC, AB= BC,∠ BAD=90°, AC交 BD于点 E,∠ ABD=30°, AD= ,求线段 AC和 BE的长.
(注: )