探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
4 |
… |
y |
… |
|
a |
﹣2 |
﹣4 |
b |
﹣4 |
﹣2 |
|
|
… |
(1)列表,写出表中 , 的值: , ;
描点、连线,在所给的平面直角坐标系中画出该函数的图象.
(2)观察函数图象,判断下列关于函数性质的结论是否正确(在答题卡相应位置正确的用“√”作答,错误的用“×”作答):
①函数 的图象关于y轴对称;
②当 时,函数 有最小值,最小值为 ;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.

在直角梯形ABCD中,∠D=90°,高CD= cm(如图1),动点P、Q同时从点A出发,点P沿AB、BC运动到点C停止,速度为1cm/s,点Q沿AD运动到点D停止,速度为2cm/s,而点P到达点B时,点Q正好到达点D,设P、Q同时从A点出发的时间为t(s)时,△APQ的面积为y(cm2)所形成的函数图象如图(2)所示,其中MN表示一条平行于X轴的线段.
cm(如图1),动点P、Q同时从点A出发,点P沿AB、BC运动到点C停止,速度为1cm/s,点Q沿AD运动到点D停止,速度为2cm/s,而点P到达点B时,点Q正好到达点D,设P、Q同时从A点出发的时间为t(s)时,△APQ的面积为y(cm2)所形成的函数图象如图(2)所示,其中MN表示一条平行于X轴的线段.
(1)求出BC的长和点M的坐标.
(2)当点P在线段AB上运动时,直线PQ截梯形所得三角形部分沿PQ向上折叠,设折叠后与梯形重叠部分的面积为S cm2,请求出S与t的函数关系式.
(3)在P、Q的整个运动过程中,将直线PQ截梯形所得三角形部分沿PQ折叠.是否存在某一时刻,使得折叠后与梯形重叠部分的面积为直角梯形ABCD面积的 ?若存在,求出t的值;若不存在,试说明理由.
?若存在,求出t的值;若不存在,试说明理由.
如图1,点A的坐标为(0,4),正比例函数y=kx(k>0).
探究1:当k=1时,则点A关于直线y=x对称的对称点坐标为 ;
当k= 时,则点A关于直线y=
时,则点A关于直线y= x对称的对称点坐标为 ;
x对称的对称点坐标为 ;
探究2:当k=2时,求点A关于直线y=2x对称的对称点坐标;
应用:如图2,直线OB:y=mx,直线OC:y= x,如y轴上点A关于OB对称的对称点为D,关于OC对称的对称点为G,当m= 时,四边形AOGD为菱形.
x,如y轴上点A关于OB对称的对称点为D,关于OC对称的对称点为G,当m= 时,四边形AOGD为菱形.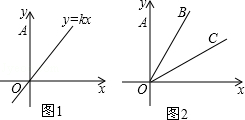
市园林处为了对一段公路进行绿化,计划购买A,B两种风景树共900棵.A,B两种树的相关信息如下表:
| 品种 项目 |
单价(元/棵) |
成活率 |
| A |
80 |
92% |
| B |
100 |
98% |
若购买A种树x棵,购树所需的总费用为y元.
(1)求y与x之间的函数关系式;
(2)若购树的总费用不超过82 000元,则购A种树不少于多少棵?
(3)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A,B两种树各多少棵?此时最低费用为多少?
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2
①求 值;
值;
②求图中阴影部分的面积.
在方格纸中,把一个图形先沿水平方向平移|a|格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为[a,b].例如,把图中的△ABC先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为[3,﹣5].若△A1B1C1经过[5,7]得到△A″B″C″.
(1)在图中画出△A″B″C″;
(2)写出△ABC经过平移得到△A″B″C″的过程 ;
(3)若△ABC经过[m,n]得到△DEF,△DEF再经过[p,q]后得到△A″B″C″,则m与p、n与q分别满足的数量关系是 , .