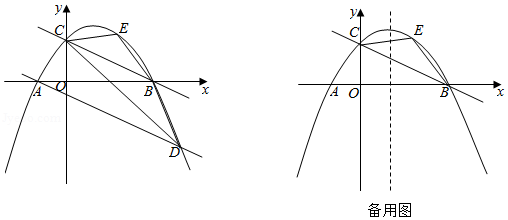
如图,在平面直角坐标系中,抛物线 与 轴交于点 ,与x轴交于 两点(点 在点 的左侧),且 点坐标为 ,直线 的解析式为 .
(1)求抛物线的解析式;
(2)过点 作 ,交抛物线于点D,点E为直线 上方抛物线上一动点,连接CE,EB,BD,DC.求四边形BECD面积的最大值及相应点E的坐标;
(3)将抛物线 向左平移 个单位,已知点 为抛物线 的对称轴上一动点,点N为平移后的抛物线上一动点.在(2)中,当四边形 的面积最大时,是否存在以 为顶点的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相应的四档高度,得到如下数据;
高度档次第一档第二档第三档第四档
凳高x(cm) 37.0 40.0 42.0 45.0
桌高y(cm) 70.0 74.8 78.0 82.8
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
某家电集团公司生产某种型号的新家电.前期投资200万元,每生产1台这种新家电,后期还需要其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(1)求总投资额y1(万元)和总利润y2(万元)关于新家电的总产量x(台)的函数关系式;
(2)当新家电的总产量为900台时,该公司的盈亏情况如何?
(3)请你利用第(1)小题中y2与x的函数关系式,分析该公司的盈亏情况.(注:总投资=前期投资+后期其他投资,总利润=总产值-总投资).
答案:
某种储蓄的月利率是0.36%,今存入本金100元,求本息和(本金与利息的和)y(元)与所存月数x之间的函数关系式,并计算5个月后的本息和。
一个铜球在0℃时的体积是1000cm3,加热后温度增加1℃,体积增加0.051cm3,写出铜球的体积V与t之间的函数关系式,并计算加热到200℃时铜球的体积.
某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油过程中,设运输飞机的油箱余量为Q1吨,加油飞机的加油油箱剩余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题: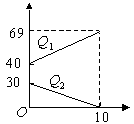
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式.