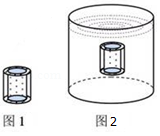
某同学制作了一个”浮子“。他用质量为 、高为 、横截面积为 的质地均匀实心圆柱体，将其中间挖掉横截面积为 、高为 的圆柱体，做成”空心管“；然后用另一个不同材质、质地均匀的实心圆柱体将管的空心部分恰好填满，做成”浮子“，如图1所示。将”浮子“放入盛有足量水、底面积为 的圆柱形薄壁容器中。”浮子“刚好悬浮在水中，如图2所示。已知水的密度为 ，请解答下列问题：
（1）该“浮子”的平均密度是多少？
（2）实验中，组成“浮子”的“空心管”和“填充柱体”在水中完全脱离，致使容器中水面高度发生了变化，待水面恢复稳定后，水对容器底部的压强变化了多少？
如图所示，轻质柱形容器甲、乙放置在水平地面上，已知甲、乙的底面积分别为2S、S。甲容器中装有3×10-2米3的水，A点离水面0.2米。
（1）求甲容器中的水的质量，A点水的压强。
（2）将乙容器中注入密度为
的液体后，甲、乙两液面相平，深度均为
，再将密度为
、体积为
的物体A放入甲容器中，将密度为、体积为
的物体B放入乙容器中（液体不溢出）。已知甲容器对地面的压强是乙容器对地面压强的3倍。求的表达式
如图所示，压力锅直径为24cm，限压出气口直径为3.5mm，限压阀质量为100g，使用时压力锅内外最大压强差是多少？锅盖与锅的接口处至少能承受多大的力？
如图所示，放置在水平地面上的两个物体A和B均为实心正方体，物体A的体积为10-3米3，物体B的边长为0.2米。物体A的密度为2×103千克/米3，物体B的质量为10千克。求：
（1）物体A的质量mA。
（2）物体B对水平地面的压强pB。
（3）在保持物体A、B原有放置方式不变的情况下，只在竖直方向上施加一个多大的力可以让两物体对地面压强相等？
质量为1千克的柱形薄壁容器放在水平面上，底面积为0.01米2，高为0.6米，装有0.5米深的酒精（ρ酒精=0.8×103千克/米3）， 如图所示。求：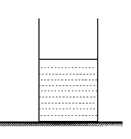
①酒精对容器底部的压强。
②容器对水平面的压强。
③在酒精中放入一个固体，保持酒精不溢出，使酒精对容器底部压强的增加量最大的情况下，同时使容器对水平面压强的增加量最小，请计算固体的质量并判断固体密度
与酒精密度
之间的大小关系，即 。
如图所示，质量均为2.4千克的薄壁圆柱形容器A和B放在水平地面上，底面积分别为2×10－2米2和1×10－2米2。容器A中盛有0.1米高的水，容器B中盛有质量为1.6千克的酒精。（ρ酒精＝0.8×103千克/米3）求：
①容器B中酒精的体积V酒精。
②容器B对水平地面的压强pB。
③现有质量相等的甲、乙两实心物块，若将甲浸没在水中、乙浸没在酒精中后，两液体均未溢出，且两液体各自对容器底部压强的变化量相等，求甲、乙的密度ρ甲、ρ乙之比。