某同学利用图（a）所示装置验证动能定理。调整木板的倾角平衡摩-优题课

某同学利用图（a）所示装置验证动能定理。调整木板的倾角平衡摩擦阻力后，挂上钩码，钩码下落，带动小车运动并打出纸带。某次实验得到的纸带及相关数据如图（b）所示。已知打出图（b）中相邻两点的时间间隔为 $0.02 s$ ，从图（b）给出的数据中可以得到，打出 $B$ 点时小车的速度大小 $v_{B} =$ 　　 $m / s$ ，打出 $P$ 点时小车的速度大小 $v_{P} =$ 　　 $m / s$ 。（结果均保留2位小数）若要验证动能定理，除了需测量钩码的质量和小车的质量外，还需要从图（b）给出的数据中求得的物理量为　　。

科目物理题型解答题难度中等

知识点：光学实验及其他探究功与速度变化的关系

如图所示，两足够长的光滑金属导轨竖直放置，相距为 $L$ ,一理想电流表与两导轨相连，匀强磁场与导轨平面垂直.一质量为 $m$ 、有效电阻为 $R$ 的导体棒在距磁场上边界 $h$ 处静止释放.导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为 $I$ 。整个运动过程中，导体棒与导轨接触良好，且始终保持水平，不计导轨的电阻。求：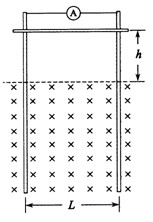

（1）磁感应强度的大小 $B$ ；
（2）电流稳定后，导体棒运动速度的大小 $v$ ；
（3）流经电流表电流的最大值 $I_{m}$

汽车行驶时轮胎的胎压太高容易造成爆胎事故，太低又会造成耗油上升。已知某型号轮胎能在－40 ${}^{o}C$ ～90 ${}^{o}C$ 正常工作，为使轮胎在此温度范围内工作时的最高胎压不超过3.5 $a t m$ ，最低胎压不低于1.6 $a t m$ ，那么在 $t ＝ 20 ° C$ 时给该轮胎充气，充气后的胎压在什么范围内比较合适？（设轮胎容积不变）

有两个完全相同的小滑块 $A$ 和 $B$ ， $A$ 沿光滑水平面以速度 $v_{0}$ 与静止在平面边缘 $O$ 点的 $B$ 发生正碰，碰撞中无机械能损失。碰后 $B$ 运动的轨迹为 $O D$ 曲线，如图所示。

（1）已知滑块质量为 $m$ ,碰撞时间为 $∆ t$ ，求碰撞过程中 $A$ 对 $B$ 平均冲力的大小。

（2）为了研究物体从光滑抛物线轨道顶端无初速下滑的运动，特制做一个与 $B$ 平抛轨道完全相同的光滑轨道，并将该轨道固定在与 $O D$ 曲线重合的位置，让 $A$ 沿该轨道无初速下滑（经分析， $A$ 下滑过程中不会脱离轨道）。
a.分析 $A$ 沿轨道下滑到任意一点的动量 $p_{A}$ 与 $B$ 平抛经过该点的动量 $p_{B}$ 的大小关系;

b.在 $O D$ 曲线上有一 $M$ 点， $O$ 和 $M$ 两点连线与竖直方向的夹角为45°。求 $A$ 通过 $M$ 点时的水平分速度和竖直分速度。

有两列简谐横波 $a$ 、 $b$ 在同一媒质中沿 $x$ 轴正方向传播，波速均为 $v ＝ 2.5 m / s$ 。在 $t ＝ 0$ 时，两列波的波峰正好在 $x ＝ 2.5 m$ 处重合，如图所示。
（1）求两列波的周期 $T_{a}$ 和 $T_{b}$ 。

（2）求 $t ＝ 0$ 时，两列波的波峰重合处的所有位置。

（3）辨析题：分析并判断在 $t ＝ 0$ 时是否存在两列波的波谷重合处。某同学分析如下：既然两列波的波峰存在重合处，那么波谷与波谷重合处也一定存在。只要找到这两列波半波长的最小公倍数，……，即可得到波谷与波谷重合处的所有位置。

你认为该同学的分析正确吗？若正确，求出这些点的位置。若不正确，指出错误处并通过计算说明理由。

两块足够大的平行金属极板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图1、图2所示（规定垂直纸面向里为磁感应强度的正方向）。在 $t = 0$ 时刻由负极板释放一个初速度为零的带负电的粒子（不计重力）。若电场强度 $E_{0}$ 、磁感应强度 $B_{0}$ 、粒子的比荷 $\frac{q}{m}$ 均已知，且 $t_{0} = \frac{2 π m}{q B_{0}}$ ，两板间距 $h = \frac{10 π^{2} m E_{0}}{q {B_{0}}^{2}}$ 。
（1）求粒子在 $0 ～ t_{0}$ 时间内的位移大小与极板间距 $h$ 的比值。

（2）求粒子在板板间做圆周运动的最大半径（用 $h$ 表示）。

（3）若板间电场强度 $E$ 随时间的变化仍如图1所示，磁场的变化改为如图3所示，试画出粒子在板间运动的轨迹图（不必写计算过程）。

试卷网试题网古诗词网作文网范文网