黔东南州某销售公司准备购进 、 两种商品，已知购进3件 商品和2件 商品，需要1100元；购进5件 商品和3件 商品，需要1750元．
（1）求 、 两种商品的进货单价分别是多少元？
（2）若该公司购进 商品200件， 商品300件，准备把这些商品全部运往甲、乙两地销售．已知每件 商品运往甲、乙两地的运费分别为20元和25元；每件 商品运往甲、乙两地的运费分别为15元和24元．若运往甲地的商品共240件，运往乙地的商品共260件．
①设运往甲地的 商品为 （件 ，投资总运费为 （元 ，请写出 与 的函数关系式；
②怎样调运 、 两种商品可使投资总费用最少？最少费用是多少元？（投资总费用 购进商品的费用 运费）
如图，正方形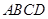
的边长为6，建立适当的平面直角坐标系，分别表示
，
，
，
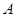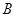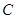四个点的坐标．
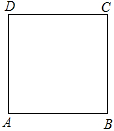
有序数对（2，3）和（3，2）相同吗？如果有序数对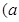
，
表示某栋楼房中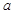
层楼
号房，那么有序数对（2，3）和（3，2）分别代表什么？
如图所示的马所处的位置为（2，3）．
⑴你能表示图中象的位置吗？
⑵写出马的下一步可以到达的位置．（马走日字）
某化工厂生产某种化肥，每吨化肥的出厂价为1780元，其成本价为900元，但在生产过程中，平均每吨化肥有280立方米有害气体排出，为保护环境，工厂须对有害气体进行处理，现有下列两种处理方案可供选择：
①将有害气体通过管道送交废气处理厂统一处理，则每立方米需付费3元；
②若自行引进处理设备处理有害气体，则每处理1立方米有害气体需原料费0.5元，且设备每月管理、损耗等费用为28000元.设工厂每月生产化肥x吨，每月利润为y元（注：利润=总收入-总支出）
（1）分别求出用方案①、方案②处理有害气体时，y与x的函数关系式；
（2）根据工厂每月化肥产量x的值，通过计算分析工厂应如何选择处理方案才能获得最大利润.
某校准备在甲、乙两家公司为毕业班学生制作一批纪念册．甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．
（1）请写出制作纪念册的册数
与甲公司的收费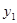
（元）的函数关系式．
（2）请写出制作纪念册的册数与甲公司的收费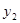
（元）的函数关系式．
（3）如果学校派你去甲、乙两甲公司订做纪念册，你会选择哪家公司？