如图是某机场监控屏显示两飞机的飞行图象，1号指挥机（看成点 始终以 的速度在离地面 高的上空匀速向右飞行，2号试飞机（看成点 一直保持在1号机 的正下方．2号机从原点 处沿 仰角爬升，到 高的 处便立刻转为水平飞行，再过 到达 处开始沿直线 降落，要求 后到达 处．
（1）求 的 关于 的函数解析式，并直接写出2号机的爬升速度；
（2）求 的 关于 的函数解析式，并预计2号机着陆点的坐标；
（3）通过计算说明两机距离 不超过 的时长是多少．
注：（1）及（2）中不必写 的取值范围
已知：如图，直线
与x轴相交于点A，与直线
相交于点P(2，
)．
(1)请判断
的形状并说明理由．
(2)动点E从原点O出发，以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合)，过点E分别作EF⊥
轴于F，EB⊥
轴于B．设运动t秒时，矩形EBOF与△OPA重叠部分的面积为S．
求：① S与t之间的函数关系式．
② 当t为何值时，S最大，并求S的最大值
如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．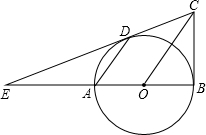
（1）求证：直线CD是⊙O的切线；
（2）若DE=2BC，AD=5，求OC的值．
如图，已知△OAB的顶点A（-6，0），B（0，2），O是坐标原点， 将△OAB绕点O按顺时针旋转90°，得到△ODC．
（1）写出C点的坐标为;
（2）设过A，D，C三点的抛物线的解析式为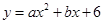
，求其解析式?
（3）证明AB⊥BE．
如图所示，秋千链子的长度为3m，静止时的秋千踏板(大小忽略不计)距地面0.5m．秋千向两边摆动时，若最大摆角(摆角指秋千链子与铅垂线的夹角)约为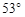
，则秋千踏板与地面的最大距离约为多少?(参考数据：
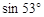≈0.8, 
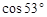≈0.6)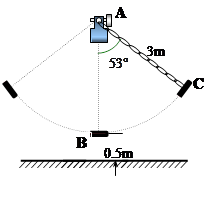
用7m长的铝合金做成透光面积（矩形ABCD的面积）为2m2的“日”型窗框（AB>BC)，求窗框的宽度?（铝合金的宽度忽略不计）