如图是某同学正在设计的一动画示意图, 轴上依次有 , , 三个点,且 ,在 上方有五个台阶 (各拐角均为 ,每个台阶的高、宽分别是1和1.5,台阶 到 轴距离 .从点 处向右上方沿抛物线 发出一个带光的点 .
(1)求点 的横坐标,且在图中补画出 轴,并直接指出点 会落在哪个台阶上;
(2)当点 落到台阶上后立即弹起,又形成了另一条与 形状相同的抛物线 ,且最大高度为11,求 的解析式,并说明其对称轴是否与台阶 有交点;
(3)在 轴上从左到右有两点 , ,且 ,从点 向上作 轴,且 .在 沿 轴左右平移时,必须保证(2)中沿抛物线 下落的点 能落在边 (包括端点)上,则点 横坐标的最大值比最小值大多少?
注:(2)中不必写 的取值范围

计算: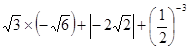
如图,在四边形ABCD中,点E、F是BC、CD的中点,且AE⊥BC,AF⊥CD.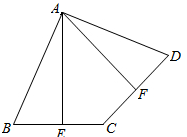
(1)求证:AB=AD.
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:

小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
解方程: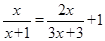 .
.
计算:
(1)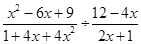
(2)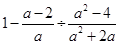 .
.