在全民健身运动中，骑行运动颇受市民青睐．一市民骑自行车由 地出发，途经 地去往 地，如图．当他由 地出发时，发现他的北偏东 方向有一信号发射塔 ．他由 地沿正东方向骑行 到达 地，此时发现信号塔 在他的北偏东 方向，然后他由 地沿北偏东 方向骑行 到达 地．
（1）求 地与信号发射塔 之间的距离；
（2）求 地与信号发射塔 之间的距离．（计算结果保留根号）
（南充）已知抛物线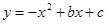
与x轴交于点A（m﹣2，0）和B（2m+1，0）（点A在点B的左侧），与y轴相交于点C，顶点为P，对称轴为l：x=1．
（1）求抛物线解析式．
（2）直线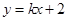
（
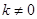）与抛物线相交于两点M（
，
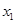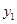），N（
，
）（
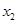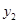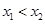），当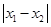
最小时，求抛物线与直线的交点M与N的坐标．
（3）首尾顺次连接点O、B、P、C构成多边形的周长为L，若线段OB在x轴上移动，求L最小值时点O，B移动后的坐标及L的最小值．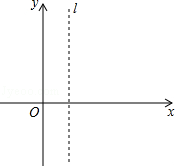
（成都）（本小题满分10分）如图，一次函数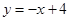
的图象与反比例函数
（
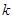为常数，且
）的图象交于A（1，a）、B两点．
（1）求反比例函数的表达式及点B的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．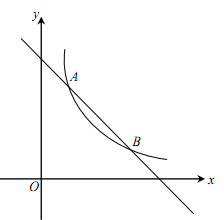
（成都）（本小题满分10分）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HG•HB的值．
（成都）（本小题满分10分）已知AC，EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90．
（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．
i）求证：△CAE∽△CBF；
ii）若BE=1，AE=2，求CE的长；
（2）如图②，当四边形ABCD和EFCG均为矩形，且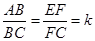
时，若BE＝1，AE=2，CE=3，求k的值；
（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）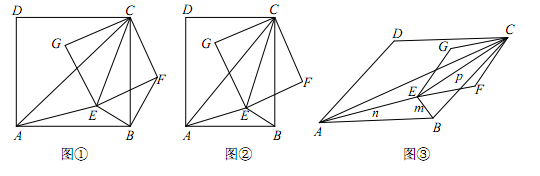
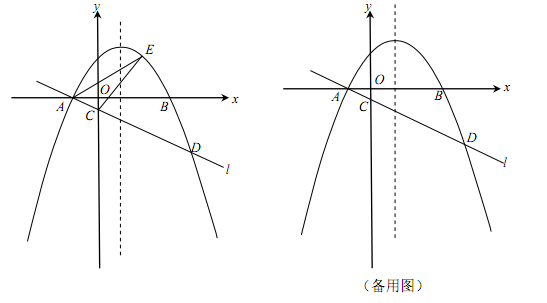
（成都）（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线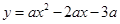
（
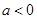）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：
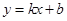与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为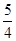
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．