已知在△ABC中,AB= ,AC=
,AC= ,BC=3.
,BC=3.
(1)如图,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图,是由100个边长为1的小正方形组成的10×10的正方形网格, 设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
(本小题12分)如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.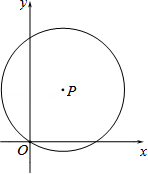
(1)若b=5,则点A坐标是;
(2)在(1)的条件下,若OQ=8,求线段BQ的长;
(3)若点P在函数y=x2(x>0)的图象上,△BQP是等腰三角形且PQ=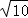
求出点B的坐标.
(本小题13分)如图,抛物线y= -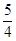 x2+
x2+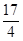 x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)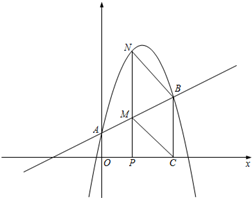
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?
(本小题12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.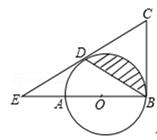
(1)求证:CD为⊙O的切线;
(2)求证:∠C=2∠DBE.
(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)
(本小题8分)一只不透明的袋子里共有4个球,其中3个白球,1个红球,它们除颜色外均相同.
(1)从袋子中随机摸出一个球是白球的概率是多少?
(2)从袋子中随机摸出一个球,不放回袋子,摇匀袋子后再摸一个球,请用列表或画树状图的方法,求出两次摸出的球都是白球的概率.
(本小题9分)如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y= +bx+c的图象经过B、C两点.
+bx+c的图象经过B、C两点.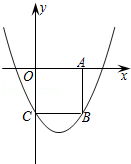
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时,x的取值范围.