问题提出
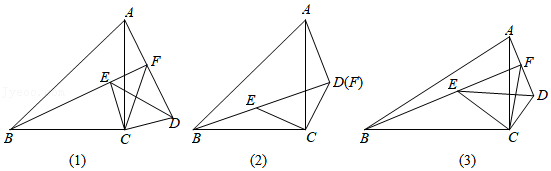
如图(1),在 和 中, , , ,点 在 内部,直线 与 于点 .线段 , , 之间存在怎样的数量关系?
问题探究
(1)先将问题特殊化如图(2),当点 , 重合时,直接写出一个等式,表示 , , 之间的数量关系;
(2)再探究一般情形如图(1),当点 , 不重合时,证明(1)中的结论仍然成立.
问题拓展
如图(3),在 和 中, , , 是常数),点 在 内部,直线 与 交于点 .直接写出一个等式,表示线段 , , 之间的数量关系.
(本题8分)我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
| 需甲种材料 |
需乙种材料 |
|
| 1件A型陶艺品 |
0.9kg |
0.3kg |
| 1件B型陶艺品 |
0.4kg |
1kg |
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有材料,分别写出八(2)班制作A型和B型陶艺品的件数.
(本题5分)若关于x的方程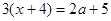 的解是关于x的方程
的解是关于x的方程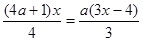 的解,求a的取值范围.
的解,求a的取值范围.
(本题8分):如图,已知AB∥CD,∠BED=90°,那么∠B+∠D等于多少度?为什么?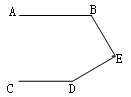
(本题5分)解分式方程: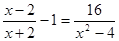
(本题5分)先化简,再求值: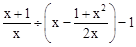 ,其中
,其中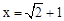 .
.