如图，在菱形ABCD中，O是对角线BD上一点(BO<DO)，-优题课

题文

如图，在菱形 $ABCD$ 中， $O$ 是对角线 $BD$ 上一点 $(BO > DO)$ ， $OE ⊥ AB$ ，垂足为 $E$ ，以 $OE$ 为半径的 $⊙ O$ 分别交 $DC$ 于点 $H$ ，交 $EO$ 的延长线于点 $F$ ， $EF$ 与 $DC$ 交于点 $G$ ．

（1）求证： $BC$ 是 $⊙ O$ 的切线；

（2）若 $G$ 是 $OF$ 的中点， $OG = 2$ ， $DG = 1$ ．

①求 $\hat{HE}$ 的长；

②求 $AD$ 的长．

科目数学题型解答题难度未知

知识点：菱形的性质相似三角形的判定与性质切线的判定弧长的计算

登录免费查看答案和解析

相关试题

如图，已知△ABC，以点O为位似中心画一个△DEF，使它与△ABC位似，且相似比为2．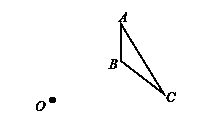

（1）2x²-9x+8=0（用公式法）
（2）3x²-4x-6=0（配方法解）
（3）（x-2）²=（2x+3）²（用合适的方法）
（4）（5x-1）²-3（5x-1）=0（用合适的方法）

如图，二次函数y=x²+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．

（1）求二次函数的解析式．
（2）求函数图象的顶点坐标及D点的坐标．
（3）该二次函数的对称轴交x轴于C点．连接BC，并延长BC交抛物线于E点，连接BD，DE，求△BDE的面积．
（4）抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S_△_ADP=S_△_BCD？若存在，请求出P点的坐标；若不存在．请说明理由．

某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？

如图所示，在抛物线y=-x²上有A，B两点，其横坐标分别为1，2；在y轴上有一动点C，使AC+BC距离最短，求C点的坐标．

试卷网试题网古诗词网作文网范文网