如图所示,抛物线与 轴交于 、 两点,与 轴交于点 ,且 , , ,抛物线的对称轴与直线 交于点 ,与 轴交于点 .
(1)求抛物线的解析式;
(2)若点 是对称轴上的一个动点,是否存在以 、 、 为顶点的三角形与 相似?若存在,求出点 的坐标,若不存在,请说明理由;
(3) 为 的中点,一个动点 从 点出发,先到达 轴上的点 ,再走到抛物线对称轴上的点 ,最后返回到点 .要使动点 走过的路程最短,请找出点 、 的位置,写出坐标,并求出最短路程.
(4)点 是抛物线上位于 轴上方的一点,点 在 轴上,是否存在以点 为直角顶点的等腰 ?若存在,求出点 的坐标,若不存在,请说明理由.

某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积为1.44m2?(设窗框宽为xm)
已知关于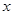 的一元二次方程
的一元二次方程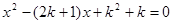 .
.
(1)求证:方程有两个不相等的实数根;
(2)若 的两边
的两边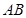 、
、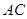 的长是方程的两个实数根,第三边
的长是方程的两个实数根,第三边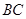 的长为
的长为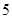 .当
.当 是等腰三角形时,求
是等腰三角形时,求 的值.
的值.
解下列关于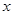 的一元二次方程
的一元二次方程
(1)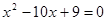
(2)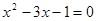
如图,在矩形 中,把点
中,把点 沿AE对折,使点
沿AE对折,使点 落在
落在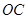 上的
上的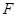 点,已知
点,已知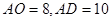 .
.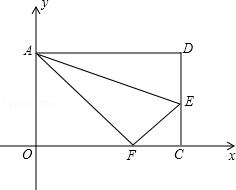
(1)求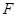 点的坐标;
点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点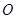 ,
,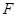 ,且直线
,且直线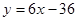 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)直线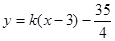 与(2)中的抛物线交于
与(2)中的抛物线交于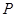 、
、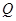 两点,点
两点,点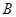 的坐标为
的坐标为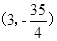 ,求证:
,求证: 为定值.
为定值.