如图①, 、 是等腰 的斜边 上的两动点, , 且 .
(1)求证: ;
(2)求证: ;
(3)如图②,作 ,垂足为 ,设 , ,不妨设 ,请利用(2)的结论证明:当 时, 成立.

甲、乙两篮球运动员上赛季每场比赛的得分如下:
甲15,24,25,31,31,36,36,37,39,44,50.
乙8,13,14,16,23,26,28,33,38,39,51.
小莉用如图的方式来表示甲、乙的得分.
(1)请在右侧补全乙的得分;
(2)用不等号填空: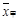
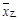 ;
;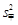
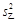 ;
;
(3)请说出此种表示方式的优点.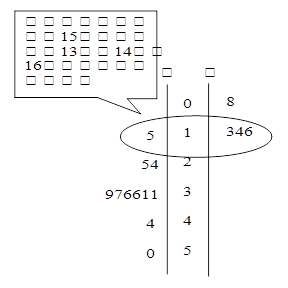
妈妈给小莉100元去超市购买笔记本,已知笔记本每本12元.
请你根据以上信息,提出一个用一元一次不等式解决的问题,并写出解答过程.
已知关于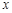 、
、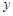 的方程组
的方程组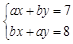 ,的解是
,的解是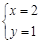 ,求
,求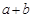 的值.
的值.
计算: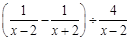 .
.
如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.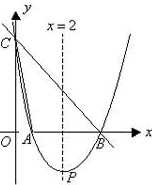
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.