《九章算术》中记载，浮箭漏（图① 出现于汉武帝时期，它由供水壶和箭壶组成，箭壶内装有箭尺，水匀速地从供水壶流到箭壶，箭壶中的水位逐渐上升，箭尺匀速上浮，可通过读取箭尺读数计算时间．某学校 小组仿制了一套浮箭漏，并从函数角度进行了如下实验探究：
【实验观察】实验小组通过观察，每2小时记录一次箭尺读数，得到如表：
供水时间 （小时） |
0 |
2 |
4 |
6 |
8 |
箭尺读数 （厘米） |
6 |
18 |
30 |
42 |
54 |
【探索发现】①建立平面直角坐标系，如图②，横轴表示供水时间 ．纵轴表示箭尺读数 ，描出以表格中数据为坐标的各点．
②观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由．
【结论应用】应用上述发现的规律估算：
①供水时间达到12小时时，箭尺的读数为多少厘米？
②如果本次实验记录的开始时间是上午 ，那当箭尺读数为90厘米时是几点钟？（箭尺最大读数为100厘米）
某渔场计划购买甲、乙两种鱼苗共6000尾，甲种鱼苗每尾0.5元，乙种鱼苗每尾0.8元．相关资料表明：甲、乙两种鱼苗的成活率分别为90%和95%．
（1）若购买这批鱼苗共用了3600元，求甲、乙两种鱼苗各购买了多少尾？
（2）若购买这批鱼苗的钱不超过4200元，应如何选购鱼苗？
（3）若要使这批鱼苗的成活率不低于93%，且购买鱼苗的总费用最低，应如何选购鱼苗？
如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取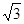
＝1.732，结果精确到1m）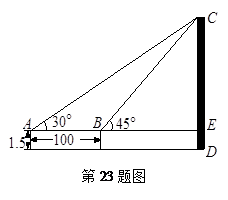
如图9所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：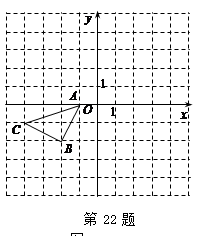
（1）分别写出点A、B两点的坐标；
（2）作出△ABC关于坐标原点成中心对称的△A1B1C1；
（3）作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部，请直接写出x的取值范围.
初中生对待学习的态度一直是教育工作者关注的问题之一．为此，某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．
请根据图中提供的信息，解答下列问题：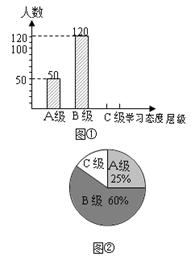
（1）此次抽样调查中，共调查了名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计该区近80000名
初中生中大约有多少名学生学习态度达标（达标包括A级和B级）？
如图，在矩形ABCD中，点E、F在BC边上，且BE=CF，AF、DE交于点M．
求证：AM=DM．