初中生对待学习的态度一直是教育工作者关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).
请根据图中提供的信息,解答下列问题: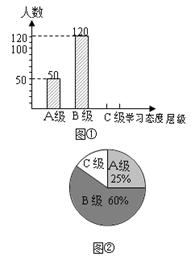
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该区近80000名
初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?
如图,在 中, , 为 边上的中线, 于点 .
(1)求证: .
(2)若 , ,求线段 的长.

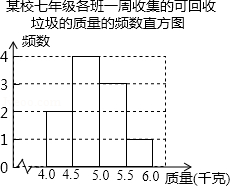
某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量的频数表
|
组别 |
频数 |
|
|
2 |
|
|
|
|
|
3 |
|
|
1 |
(1)求 的值;
(2)已知收集的可回收垃圾以0.8元 被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到50元?
已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为 (单位:吨 小时),卸完这批货物所需的时间为 (单位:小时).
(1)求 关于 的函数表达式.
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
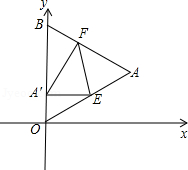
如图, 是边长为 的等边三角形,其中 是坐标原点,顶点 在 轴正方向上,将 折叠,使点 落在边 上,记为 ,折痕为 .
(1)当 轴时,求点 和 的坐标;
(2)当 轴,且抛物线 经过点 和 时,求抛物线与 轴的交点的坐标;
(3)当点 在 上运动,但不与点 、 重合时,能否使△ 成为直角三角形?若能,请求出此时点 的坐标;若不能,请你说明理由.
已知:如图, 、 是平行四边形 的对角线 上的两点, .
求证:(1) ;
(2) .
