在平面直角坐标系中，抛物线 为常数）的顶点为 ．
（1）当 时，点 的坐标是 ，抛物线与 轴交点的坐标是 ；
（2）若点 在第一象限，且 ，求此抛物线所对应的二次函数的表达式，并写出函数值 随 的增大而减小时 的取值范围；
（3）当 时，若函数 的最小值为3，求 的值；
（4）分别过点 、 作 轴的垂线，交抛物线的对称轴于点 、 ．当抛物线 与四边形 的边有两个交点时，将这两个交点分别记为点 、点 ，且点 的纵坐标大于点 的纵坐标．若点 到 轴的距离与点 到 轴的距离相等，直接写出 的值．
如图，直线y＝kx＋k（k≠0）与双曲线y＝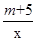
在第一象限内相交于点M，与x轴交于点A．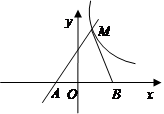
（1）求m的取值范围和点A的坐标；
（2）若点B的坐标为（3，0），AM＝5，S△ABM＝8，求双曲线的函数表达式．
如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．
(1)求证：EF是⊙O的切线；
(2)当DF：DE＝2：1时，∠BAC的度数为多少？说明理由；
如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成。已知天桥高度BC≈4.8米，引桥水平跨度AC=8米
（1）求水平平台DE的长度；
（2）若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比。
(参考：sin37°=0.60，cos37°=0.80，tan37°=0.75)
阅读对话，解答问题．
(1)分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树形图法或列表法写出(a，b)的所有取值；
(2)若小冬从小丽、小兵袋子中抽出的卡片上标有的数字之积为奇数，算小丽赢，否则算小兵赢，这样的取法合理吗？
5月19日，中国首个旅游日正式启动，某校组织了由八年级800名学生参加的旅游地理知识竞赛．李老师为了了解对旅游地理知识的掌握情况，从中随机抽取了部分同学的成绩作为样本，把成绩按优秀、良好、及格、不及格4个级别进行统计，并绘制成了如图所示的条形统计图和扇形统计图(部分信息未给出)．
请根据以上提供的信息，解答下列问题：
(1)求被抽取的部分学生的人数；
(2)请补全条形统计图，并求出扇形统计图中表示及格的扇形的圆心角度数；
(3)请估计八年级的800名学生中达到良好和优秀的总人数．