如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .
(1)当点 与点 重合时,直接写出 的长;
(2)当点 在边 上运动时,直接写出 的长(用含 的代数式表示);
(3)求
关于
的函数解析式,并写出自变量
的取值范围.
一辆汽车装满货物的卡车,2.5m的高,1.6m的宽,要进厂门形状如图某工厂,问这辆卡车能否通过门?请说明理由。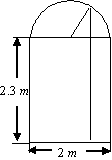
定义运算“@”如下:当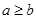 时,
时,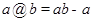 ;当
;当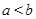 时,
时,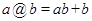 。(1)计算:
。(1)计算: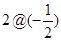 (2)若
(2)若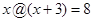 ,求x的值?
,求x的值?
已知:如图,∠B+∠DCF=180°,CM平分∠BCE,CM⊥CN,判断∠B与∠DCN的关系,并证明你的结论。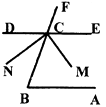
答:∠B与∠DCN的关系是
证明:
已知:如图,∠1=∠2,∠3+∠DCB=180°,∠CME:∠GEM=4:5,求∠CME的度数。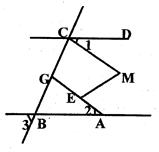
如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF//BC交AB于E、交AC于F。若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数。