【阅读】
通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是"数形结合"思想的典型应用．
【理解】
（1）如图1， ， ，垂足分别为 、 ， 是 的中点，连接 ．已知 ， ．
①分别求线段 、 的长（用含 、 的代数式表示）；
②比较大小： （填" "、" "或" " ，并用含 、 的代数式表示该大小关系．
【应用】
（2）如图2，在平面直角坐标系 中，点 、 在反比例函数 的图象上，横坐标分别为 、 ．设 ， ，记 ．
①当 ， 时， ；当 ， 时， ；
②通过归纳猜想，可得 的最小值是 ．请根据图2构造恰当的图形，并说明你的猜想成立．
请把下列各数填入相应的集合中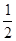
， 5.2， 0， 
， 
， 
,
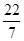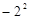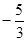，2005 , -0.030030003…
正数集合：｛…｝分数集合：｛…｝
非负整数集合：｛…｝有理数集合：｛…｝
从2开始，连续的偶数相加，它们的和的情况如下表：
加数m的个数和(S)
1 ———————————→2＝1×2
2 ————————→2＋4＝6＝2×3
3 ——————→2＋4＋6＝12＝3×4
4 ————→2＋4＋6＋8＝20＝4×5
5 ——→2＋4＋6＋8＋10＝30＝5×6
(1)按这个规律，当m＝6时，和为_______；
(2)从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：
__________________________________________．
(3)应用上述公式计算：
①2＋4＋6＋…＋200 ②202＋204＋206＋…＋300
已知A、B在数轴上分别表示a，b．
(1)对照数轴填写下表：
(2)若A、B两点间的距离记为d，试问：d和a，b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P，使它到10和－10的距离之和为20，并求所有这些整数的和；
(4)找出(3)中满足到10和－10的距离之差大于1而小于5的整数的点P；
(5)若点C表示的数为x，当点C在什么位置时，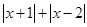
取得的值最小?
如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B(+l，+3)；从C到D记为：C→D(+1，－2)。其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（，），C→（-2，）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），请在图中标出P的位置。
根据某地实验测得的数据表明，高度每增加1 km，气温大约下降6℃，已知该地地面温度为21℃．
(1)高空某处高度是8 km，求此处的温度是多少；
(2)高空某处温度为一24 ℃，求此处的高度．