某市在实施居民用水定额管理前,对居民生活用水情况进行了调查.通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如表:
序号 |
1 |
2 |
|
25 |
26 |
|
50 |
51 |
|
75 |
76 |
|
99 |
100 |
月均用水量 |
1.3 |
1.3 |
|
4.5 |
4.5 |
|
6.4 |
6.8 |
|
11 |
13 |
|
25.6 |
28 |
(1)求这组数据的中位数.已知这组数据的平均数为 ,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使 的家庭水费支出不受影响,你觉得这个标准应该定为多少?
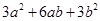
先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续正整数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)
=101×____= _______
(1)补全上述例题解题过程
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b)
观察表一,寻找规律.表二、表三分别是从表一中选取的一部分,则 ,
, 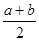 =.
=.
| 0 |
1 |
2 |
3 |
… |
| 1 |
3 |
5 |
7 |
… |
| 2 |
5 |
8 |
11 |
… |
| 3 |
7 |
11 |
15 |
… |
| … |
… |
… |
… |
… |
| 11 |
| 14 |
| a |
| 11 |
13 |
| 17 |
b |
表一表二表三
按下图方式摆放餐桌和椅子:
(1)1张餐桌可坐6个人,2张餐桌可坐___________人;
(2)按照上图的方式继续排列餐桌,完成下表:
| 桌子张数 |
4 |
5 |
… |
n |
| 可坐人数 |
… |
解方程: 