在几何体表面上，蚂蚁怎样爬行路径最短？
（1）如图①，圆锥的母线长为 ， 为母线 的中点，点 在底面圆周上， 的长为 ．在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径，并标出它的长（结果保留根号）．
（2）图③中的几何体由底面半径相同的圆锥和圆柱组成． 是圆锥的顶点，点 在圆柱的底面圆周上，设圆锥的母线长为 ，圆柱的高为 ．
①蚂蚁从点 爬行到点 的最短路径的长为 （用含 ， 的代数式表示）．
②设 的长为 ，点 在母线 上， ．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点 爬行到点 的最短路径的示意图，并写出求最短路径的长的思路．
（本小题满分8分）
一水库大坝的横截面是梯形ABCD，AD∥BC，EF为水库的水面，点E在DC上.已测得背水坡AB的长为12米，迎水坡DE的长为2米，∠BAD=135°，∠ADC=120°.试求水库的深度.（结果精确到0.1米，
）
（本题共两小题，每小题6分，满分12分）
（1）计算：
；
（2）化简：
已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．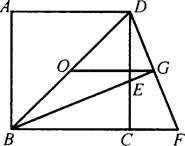
(1)说明：△BCE≌△DCF；
(2)OG与BF有什么数量关系？说明你的结论；
(3)若BC·BD＝
，求正方形ABCD的面积．
如图，P是等边三角形ABC内的一点，连结PA、PB、PC，以BP为边作等边三角形BPM，连结CM.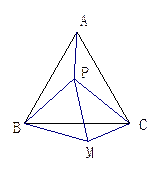
（1）观察并猜想AP与CM之间的大小关系，并说明你的结论；
（2）若PA:PB:PC=1: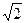
:
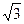，试判断△PMC的形状，并说明理由.
如图所示，∠MBN=45°，若△ABC的顶点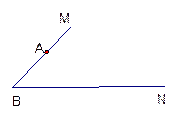
A在射线BM上，且AB=
，点C在射线BN运动（C
不与B重合）.请你探究：
（1）当BC=时，△ABC是直角三角形，并标出所有符合要求的C点；
（2）当BC的值在范围时，△ABC是锐角三角形；
（3）当BC的值在范围时，△ABC是钝角三角形 .