某学校计划在八年级开设"折扇"、"刺绣"、"剪纸"、"陶艺"四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出).

请你根据以上信息解决下列问题:
(1)参加问卷调查的学生人数为 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择"陶艺"课程的学生占 ;
(3)若该校八年级一共有1000名学生,试估计选择"刺绣"课程的学生有多少名?
如图,正方形网格中的每个小正方形的边长都是1,顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交 轴
轴
于 两点,点
两点,点 在⊙
在⊙ 上.
上.
(1)求出 两点的坐标;
两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点 ,使线段
,使线段 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上从点A运动到点B,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.
(1)求证:CE=CF;
(2)求线段EF的最小值;
(3)当点D从点A运动到点B时,线段EF扫过的面积的大小是 .
已知:如图,二次函数y=a(x﹣h)2+ 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.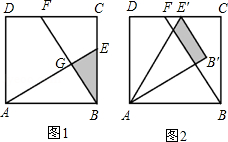
(1)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(2)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.