甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元. 乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元. |
说明:①汽车数量为整数;②月利润 月租车费 月维护费;③两公司月利润差 月利润较高公司的利润 月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是 48000 元;当每个公司租出的汽车为 辆时,两公司的月利润相等;
(2)求两公司月利润差的最大值;
(3)甲公司热心公益事业,每租出1辆汽车捐出 元 给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求 的取值范围.
(·辽宁大连)如图,在平面坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y= 经过点B.将△AOB绕点B逆时针旋转,使点O的对应点D落在X轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B.将△AOB绕点B逆时针旋转,使点O的对应点D落在X轴的正半轴上.若AB的对应线段CB恰好经过点O.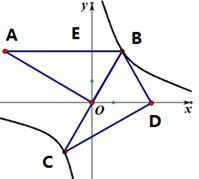
(1)点B的坐标和双曲线的解析式.
(2)判断点C是否在双曲线上,并说明理由.
(·辽宁营口)【问题探究】
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45º,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【8分】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.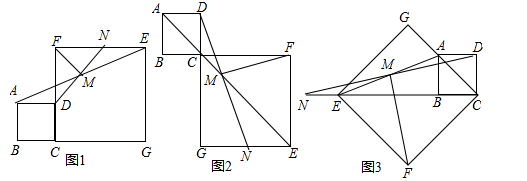
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【6分】如图,在边上为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2;
(3)求△CC1C2的面积.
(·辽宁大连)甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?