某学校九年级有12个班，每班50名学生，为了调查该校九年级学生平均每天的睡眠时间，准备从12个班里抽取50名学生作为一个样本进行分析，并规定如下：设每个学生平均每天的睡眠时间为 （单位，小时），将收集到的学生平均每天睡眠时间按 、 、 分为三类进行分析．
（1）下列抽取方法具有代表性的是 ．
．随机抽取一个班的学生
．从12个班中，随机抽取50名学生
．随机抽取50名男生
．随机抽取50名女生
（2）由上述具有代表性的抽取方法抽取50名学生，平均每天的睡眠时间数据如表：
睡眠时间 （小时） |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
8.5 |
人数（人 |
1 |
1 |
2 |
10 |
15 |
9 |
10 |
2 |
①这组数据的众数和中位数分别是 ， ；
②估计九年级学生平均每天睡眼时间 的人数大约为多少；
（3）从样本中学生平均每天眠时间 的4个学生里，随机抽取2人，画树状图或列表，求抽得2人平均每天睡眠时间都是6小时的概率．
已知抛物线 y=ax2+bx+3 （a≠0） 经过A（5，0）， B（6，1）两点，且与y轴交于点C．
（1）求抛物线y=ax2+bx+3（a≠0）的函数关系式及点C的坐标；
（2）如图（1），连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图（2），连接AC，E为线段AC上任意一点（不与A重合）经过A、E、O三点的圆交直线AB于点F，求出当△OEF的面积取得最小值时，点E的坐标．
有两个直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4
，将这两个直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．
（1）如图2，当三角板DEF运动到点D到点A重合时，设EF与BC交于点M，则∠EMC= 度；
（2）如图3，当三角板DEF运动过程中，当EF经过点C时，求FC的长；
（3）在三角板DEF运动过程中，设BF=x，两块三角板重叠部分的面积为y，求y与x的函数解析式，并求出对应的x取值范围（直接写出结果，不必写过程）．
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AC=13，BC=5，BE⊥DC交DC的延长线于点E．
（1）求证：CB是∠ECA的角平分线；
（2）求DE的长；
（3）求证：BE是⊙O的切线．
长江汽车销售公司11月份销售奇瑞牌汽车，在一定范围内，每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车，该部汽车的进价为27万元，每多售出1部，则所有售出的汽车的进价均降低0．1万元/部。月底厂家根据销售量一次性返利给销售公司，销售量在10部以内（含10部），每部返利0．5万元；销售量在10部以上，每部返利1万元。
（1）若该公司当月售出3部汽车，则每部汽车的进价为 万元；
（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车（盈利=销售利润+返利）？
如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°．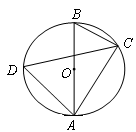
（1）求∠BAC的度数；
（2）当BC=4时，求劣弧AC的长．