阅读理解:
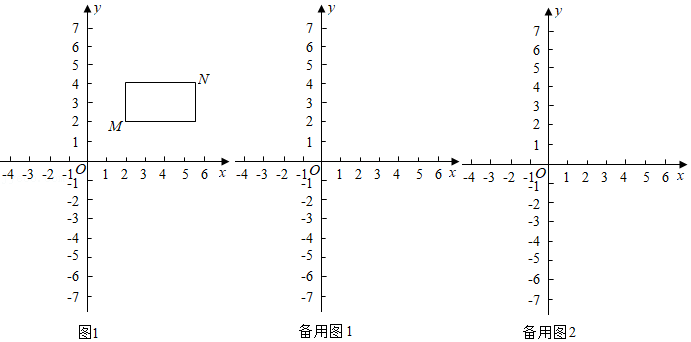
在平面直角坐标系中,点 的坐标为 , ,点 的坐标为 , ,且 , ,若 、 为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为 、 的"相关矩形".如图1中的矩形为点 、 的"相关矩形".
(1)已知点 的坐标为 .
①若点 的坐标为 ,则点 、 的"相关矩形"的周长为 ;
②若点 在直线 上,且点 、 的"相关矩形"为正方形,求直线 的解析式;
(2)已知点 的坐标为 ,点 的坐标为 若使函数 的图象与点 、 的"相关矩形"有两个公共点,直接写出 的取值.
“*”是新规定的这样一种运算法则:a*b=a2+2ab
(1)试求2*(﹣1)的值;
(2)若(﹣2)*(1*x)=x+9,求x的值.
关于x的方程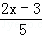 =
=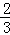 x﹣3与方程3n﹣1=3(x+n)﹣2n的解互为相反数,求n的值.
x﹣3与方程3n﹣1=3(x+n)﹣2n的解互为相反数,求n的值.
化简求值:x+2(3y2﹣2x)﹣4(2x﹣y2),其中|x﹣2|+(y+1)2=0.
计算化简或解方程:
(1)( ﹣
﹣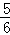 ﹣
﹣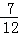 )×(﹣36)
)×(﹣36)
(2)(﹣1)3×(﹣5)÷[﹣32+(﹣2)2]
(3)5x+y﹣3(x﹣3y)
(4)3x﹣2(10﹣x)=5
(5) ﹣
﹣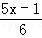 =1;
=1;
(6)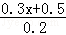 ﹣
﹣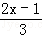 =1.
=1.
在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.
(1)仿照图1,在图2中补全672的“竖式”;
(2)仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图3所示.若这个两位数的个位数字为a,则这个两位数为 (用含a的代数式表示).