已知 和 都是等腰直角三角形 , .
(1)如图1,连接 , ,求证: ;
(2)将 绕点 顺时针旋转.
①如图2,当点 恰好在 边上时,求证: ;
②当点 , , 在同一条直线上时,若 , ,请直接写出线段 的长.

某工厂第一车间有a人 ,第二车间比第一车间人数的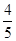 少20人,
少20人,
(1)两个车间共有多少人?
(2)如果从第二车间调出10人到第一车间,那么调动后,第一车间的人数比第二车间多多少人?
(6x2-2x)-2(x2-4x)
如图,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB 以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0)。
以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0)。(1)(2分) 当t = 2时,AP =,点Q到AC的距离是;
(2)(2+2分)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;并求出S的最大值。
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C时,请求出t的值.
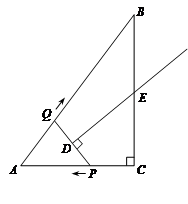
工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件 所获利润相等.
所获利润相等.(1)(4分)该工艺品每件的进价、标价分别是多少元?
(2)(6分)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则
 每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
(本小题满分8分)要在宽为28m的南滨路的路边安装路灯。路灯的灯臂长AC为3m,且与灯柱AB成120°的夹角(如图所示),路灯采用圆锥形灯罩,灯罩的轴线CD与灯臂AC垂直。当灯罩的轴线通过公路路面的中线时,照明效果最理想。问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m, )
)