在北京2008年第29届奥运会前夕，某超市在销售中发现：奥运会吉祥物—“福娃”平均每天可售出20套，每件盈利40元。为了迎接奥运会，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每套降价4元，那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元，那么每套应降价多少？
(10分)阅读下面的例题，解方程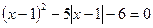
解方程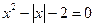
；
解：原方程化为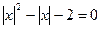
。令
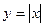，原方程化成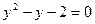
解得：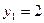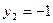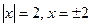
当
；当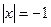
时（不合题意，舍去）
∴原方程的解是
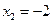
解下列方程
（1）
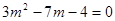（配方法） (2)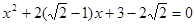
(3) 
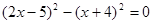
观察下列各式：
……
由上面的规律：
（1）求
的值；
（2）求
…
的个位数字．
（3）你能用其它方法求出
的值吗？
甲、乙两地同时生产某种蔬菜若干吨，现甲地可外销这种蔬菜10吨，乙地可外销这种蔬菜4吨，经调查A、B两城各需这种蔬菜分别为8吨和6吨．每吨这种蔬菜的运费如下表．设乙地运往B城的这种蔬菜为x吨．
（1）用含x的代数式来表示总运费（单位:百元/吨）；
（2）若总运费为8400元，则乙地运往A城的这种蔬菜为多少吨？
（3）试问有无可能总运费为7400元？若有可能，请写出相应的调动方案；若无可能,请说明理由.