如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 , 两点坐标分别是 , ,连接 , .
(1)求抛物线的表达式和 所在直线的表达式;
(2)将 沿 所在直线折叠,得到 ,点 的对应点 是否落在抛物线的对称轴上,若点 在对称轴上,请求出点 的坐标;若点 不在对称轴上,请说明理由;
(3)若点 是抛物线位于第三象限图象上的一动点,连接 交 于点 ,连接 , 的面积记为 , 的面积记为 ,求 的值最大时点 的坐标.

古运河是扬州的母亲河,为打造古运河风光带,现有一段河道整治任务由 两工程队完成.
两工程队完成.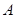 工程队单独整治该河道要16天才能完成;
工程队单独整治该河道要16天才能完成;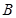 工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
(1)根据题意,万颖、刘寅两名同学分别列出尚不完整的方程如下:
万颖: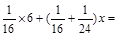
刘寅: 1
1
根据万颖、刘寅两名同学所列的方程,请你分别指出未知数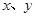 表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
万颖: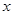 表示________________,刘寅:
表示________________,刘寅: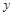 表示________________,万颖同学所列不完整的方程中的方框内该填.
表示________________,万颖同学所列不完整的方程中的方框内该填.
(2)求A工程队一共做了多少天.(写出完整的解答过程)
如图是教师每天在黑板上书写用的粉笔,请画出图示粉笔俯视图.
用小立方体重新搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则搭建这样的新几何体最少要_______个小立方块,最多要_______个小立方块.
由大小相同的小立方块搭成的几何体如图,请在下图的方格中画出该几何体的俯视图和左视图.
回答下列问题:
⑴如图所示的甲、乙两个平面图形能折什么几何体?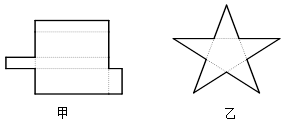
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为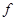 ,顶点个数为
,顶点个数为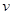 ,棱数为
,棱数为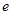 ,分别计算第(1)题中两个多面体的
,分别计算第(1)题中两个多面体的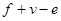 的值?你发现什么规律?
的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.