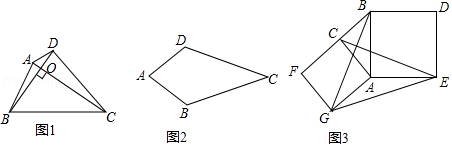
如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形 的对角线 , 交于点 .猜想: 与 有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连结 , , .已知 , ,求 的长.
如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.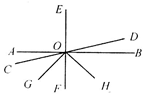
(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=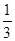 直角+
直角+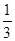 ∠BOC;②∠BOC=
∠BOC;②∠BOC=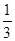 平角-
平角-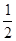 ∠AOC,问∶
∠AOC,问∶
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
如图,在灯塔A处看海岛B在南偏西50°方向,看海岛C在南偏东20°方向,在C处看海岛B在南偏西80°方向,求∠ACB的度数.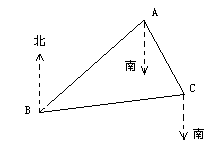
如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.求∠ADE的度数.
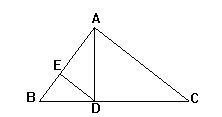
如图,△ABC中,D是BC上一点,F是BA延长线上一点,连接DF交AC于E,且∠B=42°,∠C=59°,∠DEC=47°,求∠F的度数.
