如图，在平面直角坐标系中，直线y−12x3与x轴交于点A，与-优题课

题文

如图，在平面直角坐标系中，直线 $y = - \frac{1}{2} x + 3$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = \frac{1}{3} x^{2} + bx + c$ 经过坐标原点和点 $A$ ，顶点为点 $M$ ．

（1）求抛物线的关系式及点 $M$ 的坐标；

（2）点 $E$ 是直线 $AB$ 下方的抛物线上一动点，连接 $EB$ ， $EA$ ，当 $ΔEAB$ 的面积等于 $\frac{25}{2}$ 时，求 $E$ 点的坐标；

（3）将直线 $AB$ 向下平移，得到过点 $M$ 的直线 $y = mx + n$ ，且与 $x$ 轴负半轴交于点 $C$ ，取点 $D (2, 0)$ ，连接 $DM$ ，求证： $∠ ADM - ∠ ACM = 45 °$ ．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

如图，在亚丁湾海域护航的我国A、B两艘军舰在同一条航线上航行，它们同时收到一艘商船C的求救信号，A舰发现商船在它的北偏东30º方向上，B舰发现商船在它的北偏西60º方向上。

（1）试画图确定商船C的位置
（2）求出∠ACB的度数。

解方程：（每小题4分，共8分）
（1）5x+2（3x－7）=9－4（2+x）
（2）

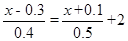
先化简，再求值：8a－[2b+6（5－b）－3a]，其中a=－3，b=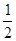

数学课上，李老师出示了如下框中的题目.
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：
AEDB（填“>”,“<”或“=”）.

（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AEDB（填“>”,“<”或“=”）.
理由如下：如图2，过点E作EF∥BC，交AC于点F.（请你接着完成以下解答过程）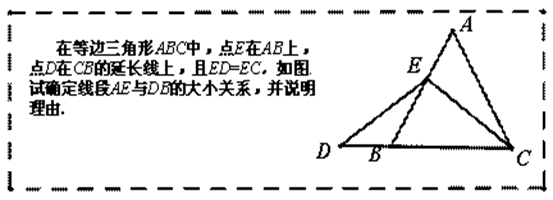

（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC.若△ABC的边长为3，AE=1，则CD的长为（请你直接写出结果）.

如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：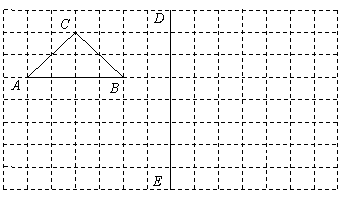

（1）画出△ABC（顶点均在格点上）关于直线DE对称的△A₁B₁C₁；
（2）在直线DE上标出一个点Q，使QA+QC的值最小．

试卷网试题网古诗词网作文网范文网