为改善城市人居环境，《成都市生活垃圾管理条例》（以下简称《条例》 于2021年3月1日起正式施行．某区域原来每天需要处理生活垃圾920吨，刚好被12个 型和10个 型预处置点位进行初筛、压缩等处理．已知一个 型点位比一个 型点位每天多处理7吨生活垃圾．
（1）求每个 型点位每天处理生活垃圾的吨数；
（2）由于《条例》的施行，垃圾分类要求提高，在每个点位每天将少处理8吨生活垃圾，同时由于市民环保意识增强，该区域每天需要处理的生活垃圾比原来少10吨．若该区域计划增设 型、 型点位共5个，试问至少需要增设几个 型点位才能当日处理完所有生活垃圾？
如图，某会展中心在会展期间准备将高5m,长13m，宽2m的楼道上铺地毯,已知地毯平方米18元，请你帮助计算一下，铺完这个楼道至少需要多少元钱? 
如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？
如图所示，在四边形ABCD 中，∠A=60°，∠B=∠D=90°，BC=2，CD=3，求AB的长.
一个零件的形状如图所示，已知AC=3
，AB=4，BD=12，求CD的长.
如图所示，无盖玻璃容器，高18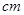
，底面周长为60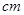，在外侧距下底1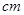的点C处有一蜘蛛，与蜘蛛相对的容器的上口外侧距开口1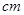的F处有一苍蝇，试求急于扑货苍蝇充饥的蜘蛛，所走的最短路线的长度.