如图1,在 中, , ,点 是 边上一点(含端点 、 ,过点 作 垂直于射线 ,垂足为 ,点 在射线 上,且 ,连接 、 .

(1)求证: ;
(2)如图2,连接 ,点 、 、 分别为线段 、 、 的中点,连接 、 、 .求 的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.
某百货大楼服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元。为了迎接“十·一”国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少?
已知关于 的方程
的方程 。
。
(1)求证此方程一定有两个不相等的实数根。
(2)设 、
、 是方程的两个实数根,且(
是方程的两个实数根,且( -2)(
-2)( -2)=2
-2)=2 ,求
,求 的值。
的值。
如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?
如图14,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为 .
.
(1)把 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的 ,画出
,画出 ,并写出
,并写出 的坐标;
的坐标;
(2)以原点 为对称中心,再画出与
为对称中心,再画出与 关于原点
关于原点 对称的
对称的 ,并写出点
,并写出点 的坐标.
的坐标.
当m为何值时,一元二次方程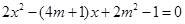 。
。
① 有两个不相等的实数根?
② 有两个相等的实数根?
③ 没有实数根?