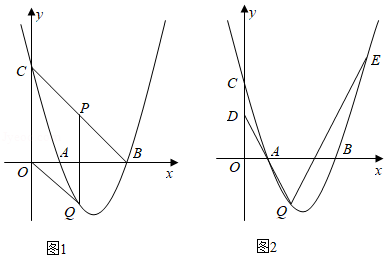
如图,已知抛物线 与 轴交于点 和 ,与 轴交于点 ,对称轴为直线 .
(1)求抛物线的解析式;
(2)如图1,若点 是线段 上的一个动点(不与点 , 重合),过点 作 轴的平行线交抛物线于点 ,连接 ,当线段 长度最大时,判断四边形 的形状并说明理由;
(3)如图2,在(2)的条件下, 是 的中点,过点 的直线与抛物线交于点 ,且 .在 轴上是否存在点 ,得 为等腰三角形?若存在,求点 的坐标;若不存在,请说明理由.
要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差 ,
, 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选参赛更合适.
图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图: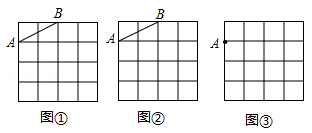
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
如图,在▱ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.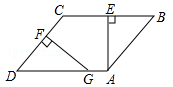
甲口袋中装有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3,4和5,从两个口袋中各随机取出1个小球.用画树状图或列表的方法,求取出的2个小球上的数字之和为6的概率.
根据图中的信息,求梅花鹿和长颈鹿现在的高度.