函数图象是研究函数的重要工具。探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程。请结合已有的学习经验,画出函数 的图象,并探究其性质.
列表如下:
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
(1)写出表中 、 的值,并在平面直角坐标系中画出该函数的图象;
(2)观察函数 的图象,判断下列关于该函数性质的命题:
①当 时,函数图象关于直线 对称;
② 时,函数有最小值,最小值为 ;
③ 时,函数 的值随 的增大而减小.
其中正确的是 .(请写出所有正确命题的番号)
(3)结合图象,请写出不等式 的解集 .

如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式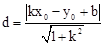 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为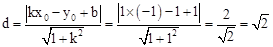 .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见表:
| 一户居民一个月用电量的范围 |
电费价格(单位:元/千瓦时) |
| 不超过160千瓦时的部分 |
x |
| 超过160千瓦时的部分 |
x+0.15 |
某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
我州实施新课程改革后,学生的自主字习、合作交流能力有很大提高.某学校为了了解学生自主学习、合作交流的具体情况,对部分学生进行了为期半个月的跟踪调査,并将调査结果分类,A:特别好;B:好;C:一般;D:较差.现将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,一共调査了名同学,其中C类女生有名;
(2)将下面的条形统计图补充完整;
(3)为了共同进步,学校想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男生、一位女生的概率.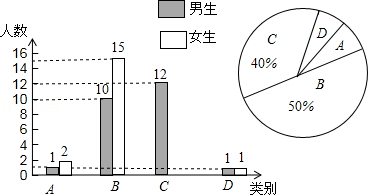
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=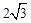 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)