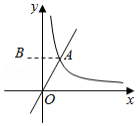
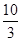在直角坐标系中,设函数 是常数, , 与函数 是常数, 的图象交于点 ,点 关于 轴的对称点为点 .
(1)若点 的坐标为 ,
①求 , 的值;
②当 时,写出 的取值范围;
(2)若点 在函数 是常数, 的图象上,求 的值.
当人造地球卫星的运行速度大于第一宇宙速度而小于第二宇宙速度时,它能环绕地球运行,已知第一宇宙速度的公式是v1=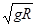 (米/秒),第二宇宙速度的公式是v2=
(米/秒),第二宇宙速度的公式是v2=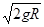 (米/秒),其中g=9.8米/秒,R=6.4×106米.试求第一、第二宇宙速度(结果保留两个有效数字).
(米/秒),其中g=9.8米/秒,R=6.4×106米.试求第一、第二宇宙速度(结果保留两个有效数字).
如图,公路MN和公路PG在点P处交汇,点A处有一所中学,且A点到MN的距离是 米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
一片矩形小树林,长是宽的3倍,而对角线的长为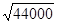 米,每棵树占地1米2,这片树林共有多少棵树?小树林的长大约是多少米?(结果精确到1米)
米,每棵树占地1米2,这片树林共有多少棵树?小树林的长大约是多少米?(结果精确到1米)
用一根长为6米的绳子,能否做一个直角△ABC,使得∠C=90°,AC=1米,BC=2米,请说明你的理由.
通过估计,比较大小: 与
与